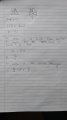[MATH] Riddle-ish Geometry help.

[Monado_III]

So tomorrow I'm going to a math contest (and skipping school), these are the finals as I already passed the preliminaries. This is the second time I'm taking it and if last year taught me anything, it's that the finals consist mostly of preliminary questions just with slighly different numbers. I was able to figure out almost every question but one and since my actual math teachers are of no help I though I'd ask here.

The question is: "A wire is cut into two pieces of equal length. One is bent to form an equilateral triangle with area 2, and the other is bent to form a regular hexagon. What is the area of the hexagon?"
Possible answers are: A) 2 B) 3/2√3 C) 3 D) 2√3 E) 4

I don't care too much about the answer but more on how you get there.

I can give you any one (or two or three) of the 3ds humble bundle games (minus SF3d) if you can help me

 

[Pedeadstrian]

Using the formula A=((rt3)/4)*a^2, you can plug in 2 for A to solve for a, which is 2.14914. Multiply 2.14914 by 3 (because there are 3 sides to a triangle) and you get a perimeter of 6.44742. Then divide that by 6 (because there are six sides to a hexagon) and you get 1.07457. Plug that into the formula A=((3*rt3)/2)*a^2 and you get 3.

So, to add my breakthrough of the steps: the two shapes are made up of the same length of wire, i.e. their perimeter is the same. Once you realize that, it's quite simple. Use the formula to find out the length of the triangle's sides, and once you have that you can use logic to determine that the length of the sides is equal to twice the length of the hexagon's sides, and then you plug that number into the formula for a hexagon.

 

[raystriker]

Basically, use the area of the triangle given, to find the length of its sides and hence the perimeter. This perimeter is equal to the perimeter of the Hexagon. Now, the perimeter of the hexagon divided by 6 gives us the length of sides. Input this length in the equation [3√3a²]/2. This is your area.

 

[yodamerlin]

Hopefully it uploaded, but here's how I did it. No calculator needed!
Notes: Internal angle of hexagon is 120 so each triangle is equilateral as 2 of the angle are 60 degrees.
This therefore only works with a hexagon.
And nice question, if you have anymore I'm up for the challenge.

 

[porkiewpyne]

Area of triangle
= ½ * b * h

Given, area of triangle = 2

Therefore,
1/2 * b * h = 2
bh = 4....................................................... Equation (1)

Also, applying Pythagoras's theorem
((1/2)b)^2 + h^2 = b^2
(1/4)b^2 + h^2 = b^2
h^2 = b^2 - (1/4)b^2 = (3/4)b^2

h = rt[(3/4)b^2] = [(rt3)/2]b......................... Equation (2)

Substitute Equation (2) into Equation (1),
b * [(rt3)/2]b = 4
[(rt3)/2]b^2 = 4
b^2 = 8/rt3
b = 2(rt2)/[3^(1/4)]

Since the length of wire for the triangle is the same as the length for the hexagon, the side of the hexagon will be half of the side of triangle (i.e. half of b)
But if you want to work it out, here it is.

Perimeter of triangle = 3b = Perimeter of hexagon
Length of one side of hexagon = 3b/6 = 0.5b = (rt2)/[3^(1/4)]

Area of hexagon
= (3/2)(rt3){(rt2)/[3^(1/4)]}^2
= 3

EDIT: Just saw yodamerlin's solution and facepalmed because I should have thought of that instead of going the long way round.

 

[Monado_III]

I do have more (took the final today), I'll upload them later if you'd like.