Ok;
I have taken a class in C++ a little over 6 years ago and haven't used it since. I have programmed in SAS, R and a number of other Statistics program language but I have completely forgot C++.
I had an idea that I can make a program that spits out arithmetic problems but it alters the difficulty based on a number of factors. Some of the factors I have thought are the number of correct answers and the time it takes to finish each question.
The idea is that a person can practice on the problems that is at their difficulty to optimize efficiency of practicing arithmetic. At it's current stage, it lets you pick how many questions you want to do (and it spits out start time). It has a variable called factor and for each correct problem the factor increases by 1 and for each wrong problem factor decreases by 1. As factor increases the difficulty increases.
What I want to do is also increase/decrease difficulty based on time. However, time is also relative per person. It may take me a second to do a problem while it may take another person 10 seconds; so how do I create the time. Also, if the problems are going to change in difficulty, that means problem 100 is gonna be a lot harder/easier than problem 30. The idea is to use statistical models to use the collected previous problems to build an expected value for the next problem. If the person takes a significant longer time to do the problem with it's expected value, it decreases the difficulty (Same thing for the inverse case).
The reason why I am building this program is to re-learn C++; also, I have always been fascinated with numbers and patterns. I used to be able to calculate arithmetic almost 100% accurate and extremely fast, however, I have lost touched with it as a lot of my studies do not involve numerical calculations. Now that I am in a PH.D. program for statistics, I wanted to take this Summer to catch up on what I used to have.
What are your opinions; anything I can do to make it interesting, know any other factors I can use to build the difficulty model?
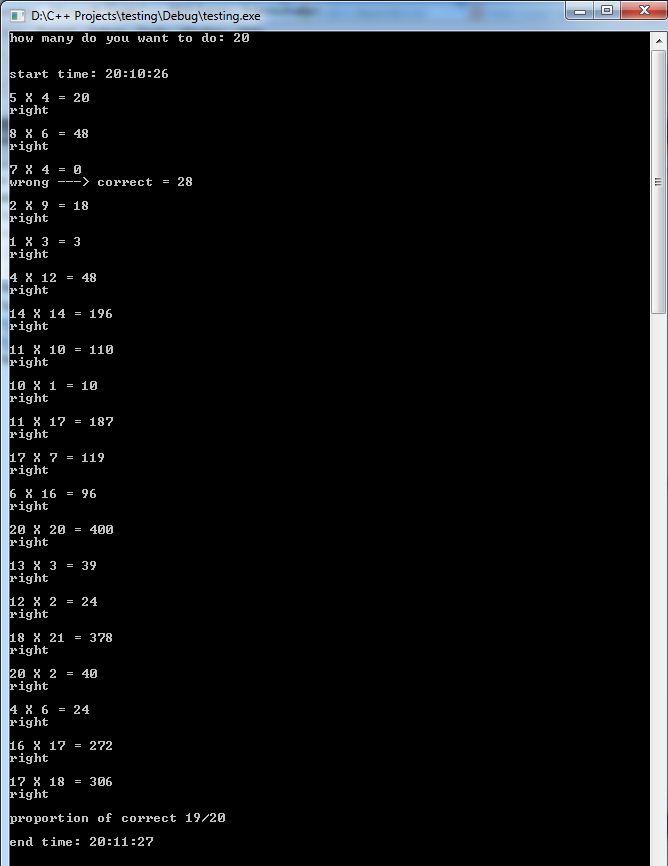
Here is a picture of it currently
I have taken a class in C++ a little over 6 years ago and haven't used it since. I have programmed in SAS, R and a number of other Statistics program language but I have completely forgot C++.
I had an idea that I can make a program that spits out arithmetic problems but it alters the difficulty based on a number of factors. Some of the factors I have thought are the number of correct answers and the time it takes to finish each question.
The idea is that a person can practice on the problems that is at their difficulty to optimize efficiency of practicing arithmetic. At it's current stage, it lets you pick how many questions you want to do (and it spits out start time). It has a variable called factor and for each correct problem the factor increases by 1 and for each wrong problem factor decreases by 1. As factor increases the difficulty increases.
What I want to do is also increase/decrease difficulty based on time. However, time is also relative per person. It may take me a second to do a problem while it may take another person 10 seconds; so how do I create the time. Also, if the problems are going to change in difficulty, that means problem 100 is gonna be a lot harder/easier than problem 30. The idea is to use statistical models to use the collected previous problems to build an expected value for the next problem. If the person takes a significant longer time to do the problem with it's expected value, it decreases the difficulty (Same thing for the inverse case).
The reason why I am building this program is to re-learn C++; also, I have always been fascinated with numbers and patterns. I used to be able to calculate arithmetic almost 100% accurate and extremely fast, however, I have lost touched with it as a lot of my studies do not involve numerical calculations. Now that I am in a PH.D. program for statistics, I wanted to take this Summer to catch up on what I used to have.
What are your opinions; anything I can do to make it interesting, know any other factors I can use to build the difficulty model?
Here is a picture of it currently
: